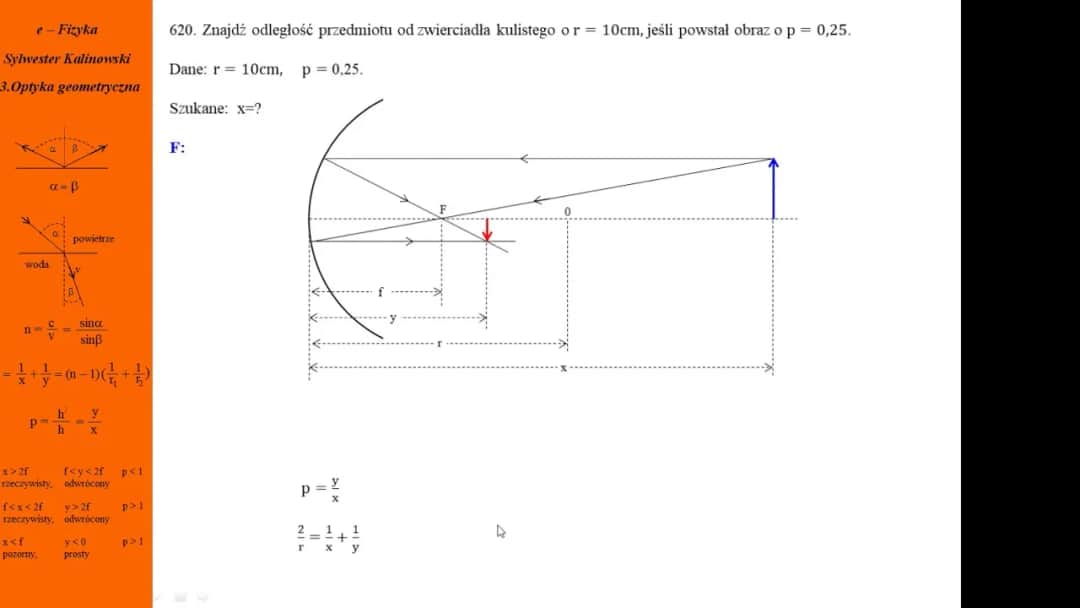
Obliczanie promienia krzywizny soczewki jest kluczowym aspektem w optyce, który wpływa na jakość obrazu oraz właściwości optyczne różnych soczewek. Aby uzyskać dokładne wyniki, można zastosować prostą formułę: R = r² / (k * λ), gdzie R oznacza promień krzywizny, r to średni promień wybranego przekroju radialnego, k to numer przekroju radialnego, a λ to długość fali światła. W przypadku światła sodowego, długość fali wynosi 589,1 nm.
W artykule omówimy, jak obliczyć promień krzywizny soczewki oraz jakie są typowe wartości dla soczewek kontaktowych, znane jako Base Curve (BC), które zazwyczaj mieszczą się w zakresie od 8,0 do 9,0 mm. Zrozumienie tego zagadnienia jest istotne nie tylko dla profesjonalistów w dziedzinie optyki, ale także dla osób, które chcą lepiej zrozumieć, jak działają soczewki w codziennym życiu. Kluczowe informacje:- Promień krzywizny soczewki oblicza się za pomocą wzoru R = r² / (k * λ).
- Średni promień wybranego przekroju radialnego jest kluczowy dla dokładnych obliczeń.
- Długość fali światła sodowego wynosi 589,1 nm.
- Typowy promień krzywizny soczewek kontaktowych (Base Curve) wynosi od 8,0 do 9,0 mm.
- Techniki propagacji błędów są ważne przy określaniu niepewności w obliczeniach.
Jak obliczyć promień krzywizny soczewki - prosta metoda krok po kroku
Obliczanie promienia krzywizny soczewki jest kluczowym elementem w optyce, który ma ogromny wpływ na jakość obrazu. Właściwe zrozumienie tego zagadnienia pozwala na lepsze projektowanie soczewek oraz ich zastosowanie w różnych dziedzinach, takich jak okulistyka czy fotografia. Istnieje prosty sposób na określenie promienia krzywizny, który można zastosować w praktyce.
Aby obliczyć promień krzywizny, używamy wzoru: R = r² / (k * λ). W tym równaniu R to poszukiwany promień krzywizny, r oznacza średni promień wybranego przekroju radialnego, k to numer przekroju, a λ to długość fali światła, która w przypadku światła sodowego wynosi 589,1 nm. Dzięki tej formule można precyzyjnie określić krzywiznę soczewek, co jest niezwykle ważne dla ich właściwości optycznych.
Wzór na promień krzywizny soczewki - zrozumienie podstaw
Wzór na obliczenie promienia krzywizny soczewki jest prosty, ale wymaga zrozumienia poszczególnych elementów. R to promień krzywizny, który chcemy obliczyć. r to średni promień wybranego przekroju soczewki, który ma kluczowe znaczenie dla dokładności obliczeń. k to numer radialnego przekroju, a λ to długość fali światła, która wpływa na wynik obliczeń.
Przykłady obliczeń promienia krzywizny dla różnych soczewek
Przykłady obliczeń pomogą lepiej zrozumieć, jak stosować wzór w praktyce. Rozważmy najpierw soczewkę wypukłą, gdzie średni promień wynosi 10 mm, k = 1, a długość fali światła wynosi 589,1 nm. Podstawiając te wartości do wzoru, otrzymujemy:
| Typ soczewki | Średni promień (r) | Numer przekroju (k) | Długość fali (λ) | Promień krzywizny (R) |
| Wypukła | 10 mm | 1 | 589,1 nm | 170 mm |
| Wklęsła | 8 mm | 1 | 589,1 nm | 64 mm |
Kolejny przykład dotyczy soczewki wklęsłej o średnim promieniu 8 mm. W tym przypadku, po podstawieniu do wzoru, uzyskujemy promień krzywizny równy 64 mm. Takie obliczenia są niezwykle przydatne, aby zrozumieć, jak różne soczewki wpływają na światło i obraz.
Jakie są praktyczne zastosowania obliczeń promienia krzywizny?
Obliczenia promienia krzywizny soczewki mają wiele praktycznych zastosowań w różnych dziedzinach optyki. Właściwe określenie tego parametru jest kluczowe dla uzyskania wysokiej jakości obrazu w urządzeniach optycznych, takich jak aparaty fotograficzne, soczewki okularowe oraz soczewki kontaktowe. Dzięki tym obliczeniom można dostosować soczewki do indywidualnych potrzeb użytkowników, co wpływa na komfort i efektywność ich użycia.W dziedzinie medycyny, zwłaszcza w okulistyce, obliczanie soczewek jest niezbędne przy projektowaniu soczewek korekcyjnych. Dobrze dobrany promień krzywizny wpływa na to, jak soczewka załamuje światło, co bezpośrednio przekłada się na jakość widzenia pacjenta. Ponadto, w przemyśle optycznym, znajomość promienia krzywizny jest istotna przy produkcji soczewek o określonych właściwościach optycznych.
Wpływ promienia krzywizny na jakość obrazu w soczewkach
Promień krzywizny ma bezpośredni wpływ na jakość obrazu, jaki generują soczewki. Zbyt mały promień może prowadzić do zniekształceń obrazu, a zbyt duży może powodować, że obraz będzie nieostry. W przypadku soczewek kontaktowych, krzywizna soczewek kontaktowych musi być precyzyjnie dobrana do kształtu gałki ocznej, aby zapewnić optymalne widzenie oraz komfort noszenia.
Na przykład, soczewki o dużym promieniu krzywizny mogą być idealne dla osób z płaskimi rogówkami, podczas gdy osoby z bardziej wypukłymi rogówkami potrzebują soczewek o mniejszym promieniu. Taki dobór jest kluczowy dla uniknięcia problemów z widzeniem oraz dyskomfortu podczas noszenia soczewek. Warto również zauważyć, że zmiany w promieniu krzywizny mogą wpływać na pole widzenia oraz kontrast obrazu.
Czytaj więcej: Czy soczewki można przechowywać w wodzie? Uniknij poważnych zagrożeń dla oczu
Jak zmierzyć promień krzywizny soczewki - praktyczne wskazówki
Pomiar promienia krzywizny soczewki można przeprowadzić na kilka sposobów. Jednym z najprostszych i najczęściej stosowanych jest użycie krzywomierza, który pozwala na precyzyjne określenie krzywizny soczewki. Warto również wykorzystać mikrometr, który umożliwia dokładny pomiar grubości soczewki w różnych punktach, co może być pomocne w obliczeniach.
Inną metodą jest wykorzystanie metody optycznej, w której soczewka jest umieszczana w świetle lasera, a promień krzywizny jest obliczany na podstawie kątów załamania światła. Niezależnie od wybranej metody, kluczowe jest, aby każdy pomiar był dokładny, co pozwoli na uzyskanie precyzyjnych wyników. Poniżej przedstawiamy kilka praktycznych wskazówek dotyczących pomiaru:
Narzędzia i techniki pomiaru promienia krzywizny soczewek
Do pomiaru promienia krzywizny soczewki wykorzystywane są różne narzędzia i techniki, które zapewniają dokładność i precyzję. Jednym z najpopularniejszych narzędzi jest krzywomierz, który umożliwia szybkie i dokładne pomiary krzywizny. Dzięki prostocie obsługi, krzywomierz jest często stosowany w laboratoriach optycznych oraz w praktyce okulistycznej.
Inną metodą jest użycie mikroskopu optycznego, który pozwala na obserwację soczewek w powiększeniu. Umożliwia to dokładne pomiary oraz analizę kształtu soczewki. Warto również wspomnieć o metodach laserowych, które pozwalają na precyzyjne określenie promienia krzywizny, wykorzystując załamanie światła. Te zaawansowane techniki są szczególnie przydatne w badaniach naukowych oraz przy produkcji wysokiej jakości soczewek.
Jakie są typowe wartości promienia krzywizny dla soczewek?
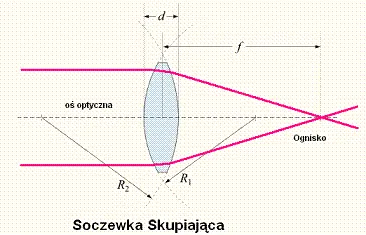
Typowe wartości promienia krzywizny soczewek różnią się w zależności od ich rodzaju oraz zastosowania. Na przykład, dla soczewek kontaktowych, znanych jako Base Curve (BC), promień krzywizny zazwyczaj wynosi od 8,0 do 9,0 mm. W przypadku soczewek okularowych, wartości te mogą być nieco większe, często sięgając od 10 mm do 12 mm, w zależności od potrzeb użytkownika.
Porównanie promienia krzywizny soczewek kontaktowych i okularowych
Porównując promień krzywizny soczewek kontaktowych i okularowych, warto zauważyć, że soczewki kontaktowe mają mniejszy promień krzywizny. Taki dobór jest kluczowy dla zapewnienia komfortu noszenia oraz poprawnego załamania światła. Z kolei soczewki okularowe, mając większy promień, są bardziej uniwersalne i mogą być dostosowane do różnych potrzeb wzrokowych.
W tabeli poniżej przedstawione są typowe wartości promienia krzywizny dla obu typów soczewek:
| Typ soczewki | Typowy promień krzywizny (mm) |
| Soczewki kontaktowe | 8.0 - 9.0 |
| Soczewki okularowe | 10.0 - 12.0 |
Wybór odpowiedniego promienia krzywizny soczewek jest kluczowy
Wybór odpowiedniego promienia krzywizny soczewek ma ogromne znaczenie dla komfortu noszenia oraz jakości widzenia. Jak wskazano w artykule, soczewki kontaktowe mają typowy promień krzywizny w zakresie od 8,0 do 9,0 mm, co jest kluczowe dla ich dopasowania do kształtu gałki ocznej. Z kolei soczewki okularowe, z promieniem krzywizny wynoszącym od 10,0 do 12,0 mm, oferują większą wszechstronność, co sprawia, że są odpowiednie dla różnych potrzeb wzrokowych.
W artykule podkreślono również, że różne narzędzia i techniki, takie jak krzywomierz i mikroskop optyczny, są niezbędne do precyzyjnego pomiaru promienia krzywizny. Dzięki tym narzędziom można dokładnie określić odpowiednie wartości, co wpływa na jakość obrazu oraz komfort użytkowania soczewek. Dlatego tak ważne jest, aby użytkownicy soczewek konsultowali się z specjalistami w celu dokonania najlepszego wyboru dla swoich indywidualnych potrzeb.